Čo je Thiessenov polygón?
Saxian senátor Tysonov polygón, nazývaný aj Voronoiov diagram (Voronoiov diagram), pomenovaný po Georgy Voronojovi, je špeciálnou formou rozdelenia priestoru.

Jeho vnútorná logika je množina súvislých polygónov zložených z vertikálnych osí spájajúcich dva susedné bodové úsečky. Vzdialenosť od ľubovoľného bodu v Thiessenovom polygóne ku kontrolnému bodu, ktorý tvorí polygón, je menšia ako vzdialenosť ku kontrolným bodom ostatných polygónov a každý polygón obsahuje jednu a len jednu vzorku.
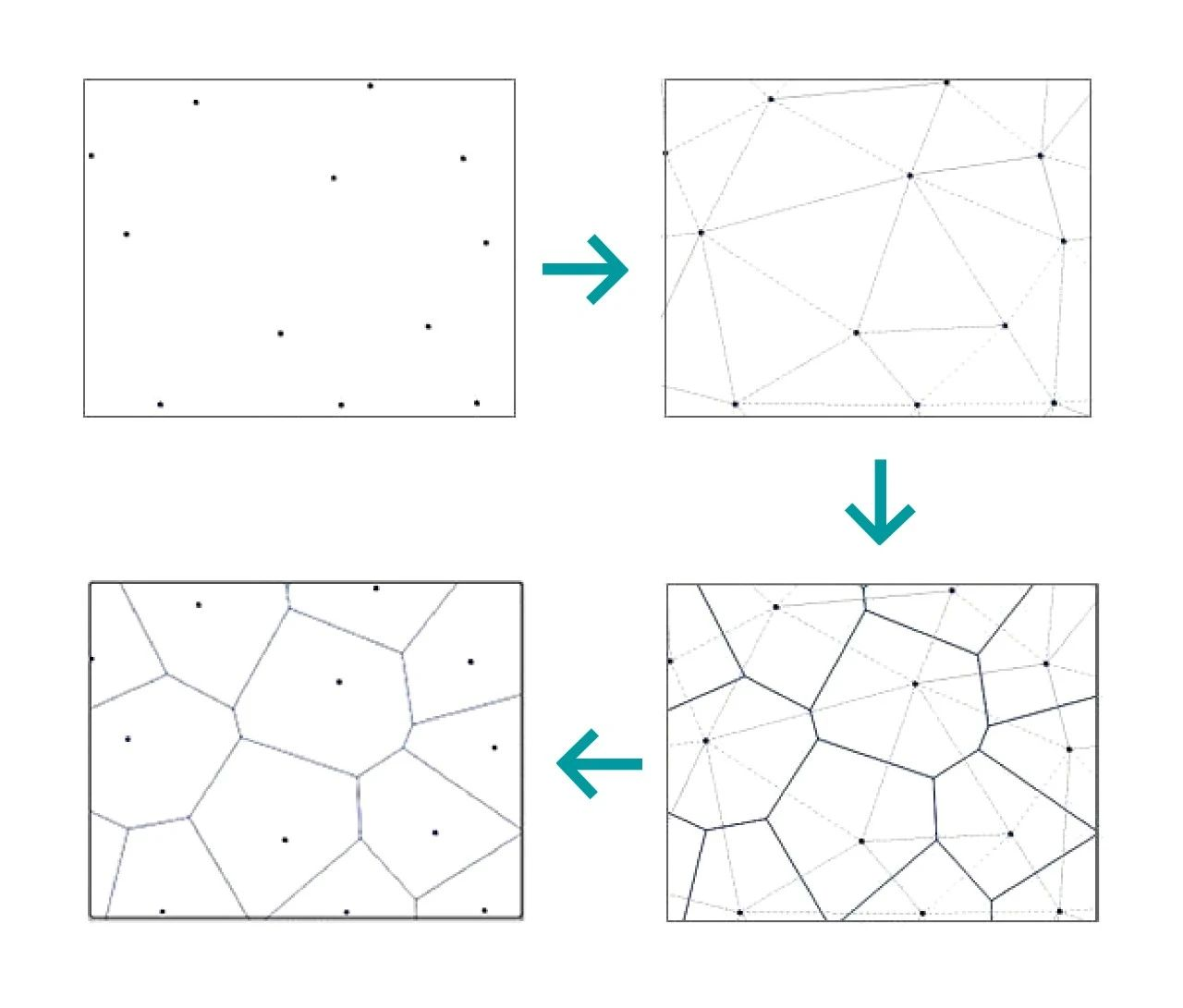
Jedinečný a nádherný vzhľad Tysonových polygónov má uplatnenie v architektúre atď. Vzhľad vodnej kocky a krajinný dizajn parkov sú aplikované na Tysonove polygóny.


Princíp miešania svetla Tyson polygónmi:
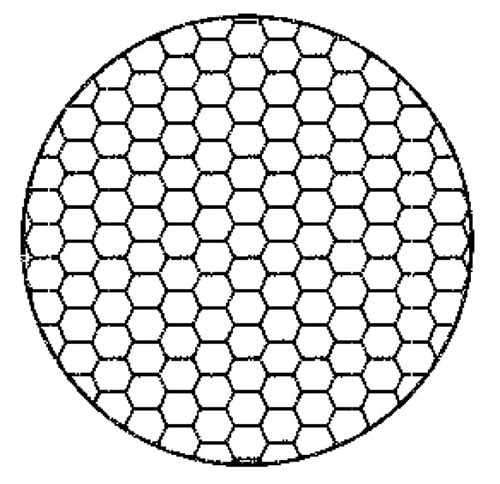
V súčasnosti šošovky na trhu často používajú štvoruholníkové, šesťuholníkové a iné guľôčkové povrchy na miešanie svetla a všetky tieto štruktúry majú pravidelný tvar.
Svetlo vyžarované svetelným zdrojom je rozdelené každou malou guľôčkovou plochou cez šošovku a nakoniec je superponované na prijímaciu plochu, čím sa vytvorí svetelná škvrna. Guľôčkové plochy rôznych tvarov môžu mapovať rôzne svetelné škvrny, takže sa používajú guľôčkové plochy s pravidelnými tvarmi, ako sú štvoruholníky a šesťuholníky. Vytvorená svetelná škvrna je tiež vytvorená superpozíciou viacerých štvoruholníkových a šesťuholníkových svetelných škvŕn.
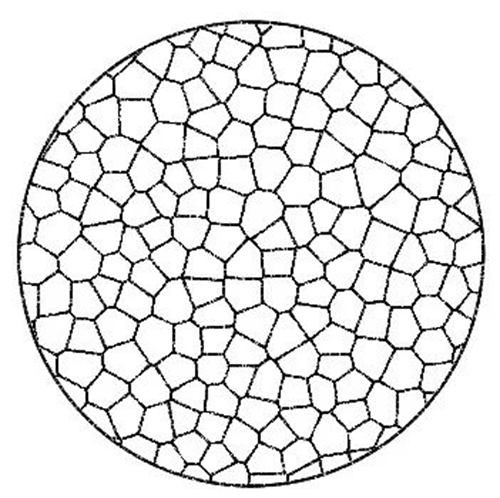
Povrch guľôčok Thiessenovho polygónu využíva nekonzistentný tvar každého Thiessenovho polygónu na prekrývanie a vytvorenie svetelnej škvrny. Keď má povrch guľôčok dostatočný počet, je možné ich prekrývať a vytvoriť rovnomernú kruhovú svetelnú škvrnu.
Bodový kontrast
Obrázok nižšie zobrazuje svetelnú škvrnu vytvorenú superpozíciou troch guľôčkových povrchov: štvoruholníka, šesťuholníka a Thiessenovho polygónu, pričom počet guľôčkových povrchov a polomer R troch typov guľôčkových povrchov sú rovnaké pod rovnakou plochou vyžarujúcou svetlo.

štvoruholníková korálková plocha

Šesťuholníková korálková plocha

Tysonova polygónová korálková tvár
Z porovnania troch svetelných bodov na obrázku vyššie je zrejmé, že svetelná škvrna vytvorená superpozíciou Tysonových polygónov na pravom obrázku je bližšie ku kruhu a svetelná škvrna bude rovnomernejšia. Je vidieť, že schopnosť miešania svetla povrchu Tysonových polygónových guľôčok je silnejšia.
Polygonálny objektív Shinland Tyson
Čas uverejnenia: 10. júna 2022








