Czym jest wielokąt Thiessena?
Wielokąt Tysona Saksońskiego Senatu, nazywany również diagramem Woronoja (Voronoi diagram), nazwany na cześć Gieorgija Woronoja, jest szczególną formą podziału przestrzeni.

Jego wewnętrzna logika to zbiór ciągłych wielokątów, składających się z dwusiecznych pionowych łączących dwa sąsiednie odcinki punktów. Odległość od dowolnego punktu wielokąta Thiessena do punktu kontrolnego, który tworzy ten wielokąt, jest mniejsza niż odległość do punktów kontrolnych innych wielokątów, a każdy wielokąt zawiera jedną i tylko jedną próbkę.
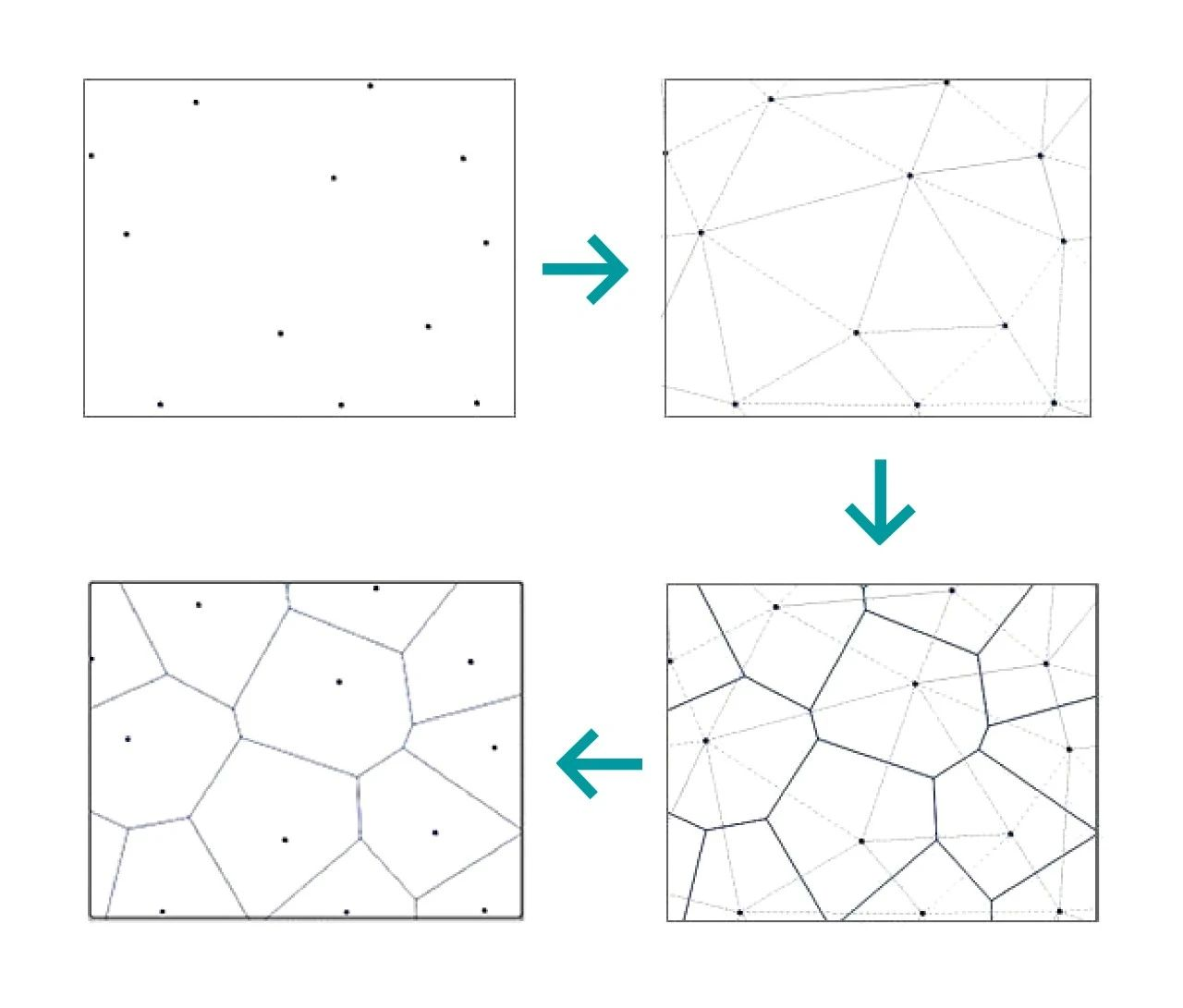
Niepowtarzalny i wspaniały wygląd wielokątów Tysona znajduje zastosowanie w architekturze itp. Wygląd sześcianu wody i projektowanie krajobrazu parków są wykorzystywane w wielokątach Tysona.


Zasada mieszania światła wielokątnego Tysona:
Obecnie dostępne na rynku soczewki często wykorzystują czworokątne, sześciokątne i inne powierzchnie koralikowe służące do mieszania światła. Wszystkie te struktury mają regularne kształty.
Światło emitowane przez źródło światła jest dzielone przez każdą małą powierzchnię koralika przez soczewkę, a następnie nakładane na powierzchnię odbiorczą, tworząc plamkę świetlną. Powierzchnie koralików o różnych kształtach mogą odwzorowywać różne plamki świetlne, dlatego stosuje się powierzchnie koralików o regularnych kształtach, takich jak czworokąty i sześciokąty. Utworzona plamka świetlna powstaje również poprzez nałożenie na siebie wielu czworokątnych i sześciokątnych plamek świetlnych.
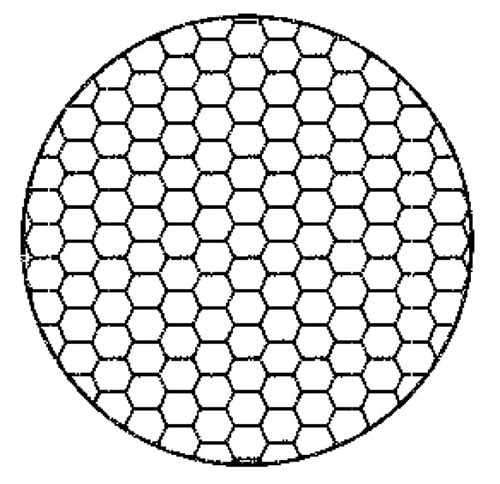
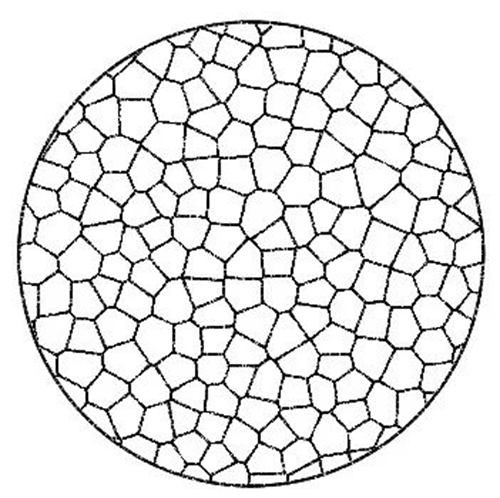
Powierzchnia koralików Thiessena z wielokątów wykorzystuje niespójny kształt każdego z nich do nałożenia na siebie, tworząc punkt świetlny. Gdy powierzchnia koralików ma wystarczającą liczbę koralików, można je nałożyć na siebie, tworząc jednolity, okrągły punkt świetlny.
Kontrast punktowy
Poniższy rysunek pokazuje plamkę świetlną utworzoną w wyniku nałożenia się trzech powierzchni koralików: czworokąta, sześciokąta i wielokąta Thiessena. Liczba powierzchni koralików i promień R trzech typów powierzchni koralików są takie same w tej samej powierzchni emitującej światło.

czworokątna powierzchnia koralikowa

Sześciokątna powierzchnia koralika

Tyson Polygon Bead Face
Z porównania trzech punktów świetlnych na powyższym obrazku wynika, że punkt świetlny utworzony przez nałożenie wielokątów Tysona na obrazku po prawej stronie jest bliższy okręgowi, a sam punkt świetlny będzie bardziej jednorodny. Widać, że zdolność mieszania światła powierzchni wielokątów Tysona jest silniejsza.
Obiektyw wielokątny Shinland Tyson
Czas publikacji: 10 czerwca 2022 r.








