Τι είναι ένα πολύγωνο Thiessen;
Το πολύγωνο Saxian Sen. Tyson ονομάζεται επίσης διάγραμμα Voronoi (διάγραμμα Voronoi), που πήρε το όνομά του από τον Georgy Voronoi, είναι μια ειδική μορφή διαίρεσης χώρου.

Η εσωτερική του λογική είναι ένα σύνολο συνεχών πολυγώνων που αποτελούνται από κάθετες διχοτόμους που συνδέουν δύο γειτονικά τμήματα σημειακής γραμμής. Η απόσταση από οποιοδήποτε σημείο σε ένα πολύγωνο Thiessen μέχρι το σημείο ελέγχου που αποτελεί το πολύγωνο είναι μικρότερη από την απόσταση από τα σημεία ελέγχου άλλων πολυγώνων, και κάθε πολύγωνο περιέχει ένα και μόνο ένα δείγμα.
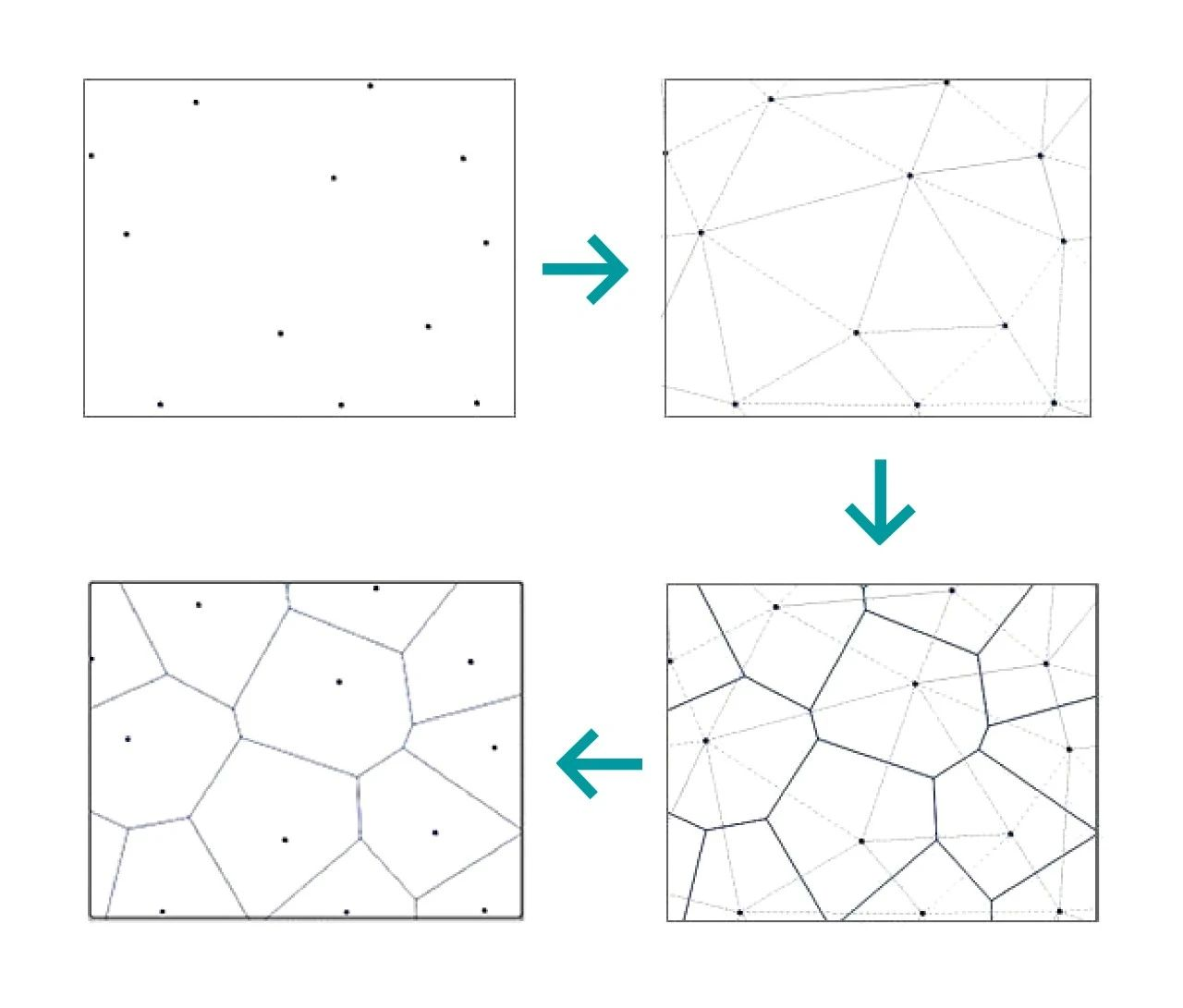
Η μοναδική και υπέροχη εμφάνιση των πολυγώνων Tyson έχει εφαρμογές στην αρχιτεκτονική κ.λπ. Η εμφάνιση του κύβου νερού και ο σχεδιασμός τοπίου των πάρκων εφαρμόζονται όλα στα πολύγωνα Tyson.


Η αρχή της ανάμειξης φωτός πολυγώνου Tyson:
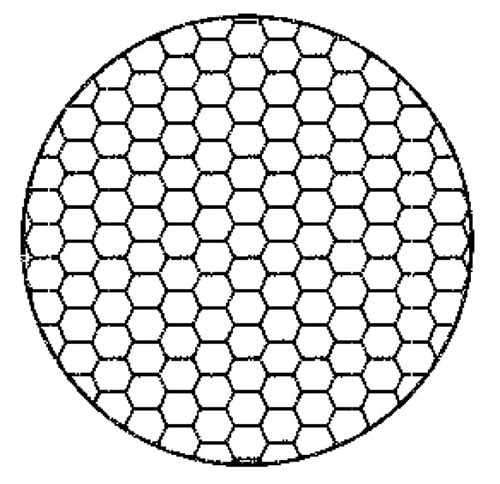
Προς το παρόν, οι φακοί στην αγορά χρησιμοποιούν συχνά τετράπλευρες, εξαγωνικές και άλλες επιφάνειες σφαιριδίων για την ανάμειξη φωτός, και αυτές οι δομές έχουν όλες κανονικά σχήματα.
Το φως που εκπέμπεται από την πηγή φωτός υποδιαιρείται από κάθε μικρή επιφάνεια σφαιριδίου που διέρχεται από τον φακό και τελικά επικαλύπτεται στην επιφάνεια λήψης για να σχηματίσει μια φωτεινή κηλίδα. Οι επιφάνειες σφαιριδίων διαφορετικών σχημάτων μπορούν να αντιστοιχίσουν διαφορετικές φωτεινές κηλίδες, επομένως χρησιμοποιούνται οι επιφάνειες σφαιριδίων με κανονικά σχήματα, όπως τετράπλευρα και εξάγωνα. Η σχηματισμένη φωτεινή κηλίδα σχηματίζεται επίσης από την υπέρθεση πλήθους τετραγωνικών και εξαγωνικών φωτεινών κηλίδων.
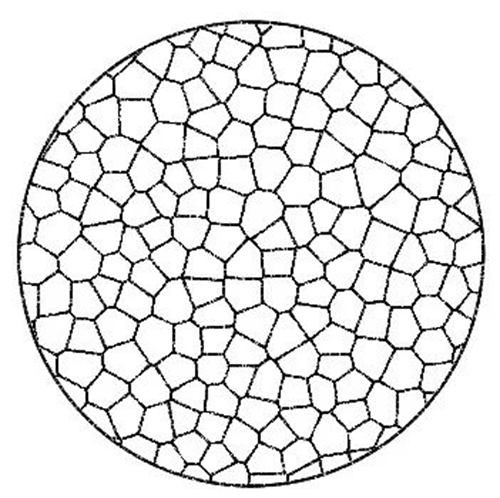
Η επιφάνεια της χάντρας πολυγώνου Thiessen χρησιμοποιεί το ασυνεπές σχήμα κάθε πολυγώνου Thiessen για να υπερτεθεί και να σχηματίσει μια φωτεινή κηλίδα. Όταν η επιφάνεια της χάντρας έχει επαρκή αριθμό, μπορεί να υπερτεθεί για να σχηματίσει μια ομοιόμορφη κυκλική φωτεινή κηλίδα.
Αντίθεση σημείων
Το παρακάτω σχήμα δείχνει την κηλίδα φωτός που σχηματίζεται από την υπέρθεση τριών επιφανειών σφαιριδίων: τετράπλευρο, εξάγωνο και πολύγωνο Thiessen, και ο αριθμός των επιφανειών σφαιριδίων και η ακτίνα R των τριών τύπων επιφανειών σφαιριδίων είναι τα ίδια κάτω από την ίδια περιοχή εκπομπής φωτός.

τετράπλευρη όψη χάντρας

Εξαγωνική όψη με χάντρες

Πρόσωπο με χάντρες Tyson Polygon
Από τη σύγκριση των τριών φωτεινών κηλίδων στην παραπάνω εικόνα, είναι προφανές ότι η φωτεινή κηλίδα που σχηματίζεται από την υπέρθεση των πολυγώνων Tyson στη δεξιά εικόνα είναι πιο κοντά σε έναν κύκλο και η φωτεινή κηλίδα θα είναι πιο ομοιόμορφη. Μπορεί να φανεί ότι η ικανότητα ανάμειξης φωτός της επιφάνειας των σφαιριδίων του πολυγώνου Tyson είναι ισχυρότερη.
Φακός πολυγώνου Shinland Tyson
Ώρα δημοσίευσης: 10 Ιουνίου 2022








