Co je Thiessenův polygon?
Saxianský polygon senátora Tysona, nazývaný také Voronojův diagram (Voronojův diagram), pojmenovaný po Georgijovi Voronojovi, je speciální formou rozdělení prostoru.

Jeho vnitřní logika je sada spojitých polygonů složených ze svislých os spojujících dva sousední bodové úsečky. Vzdálenost od libovolného bodu v Thiessenově polygonu k kontrolnímu bodu, který tvoří polygon, je menší než vzdálenost od kontrolních bodů ostatních polygonů a každý polygon obsahuje jeden a pouze jeden vzorek.
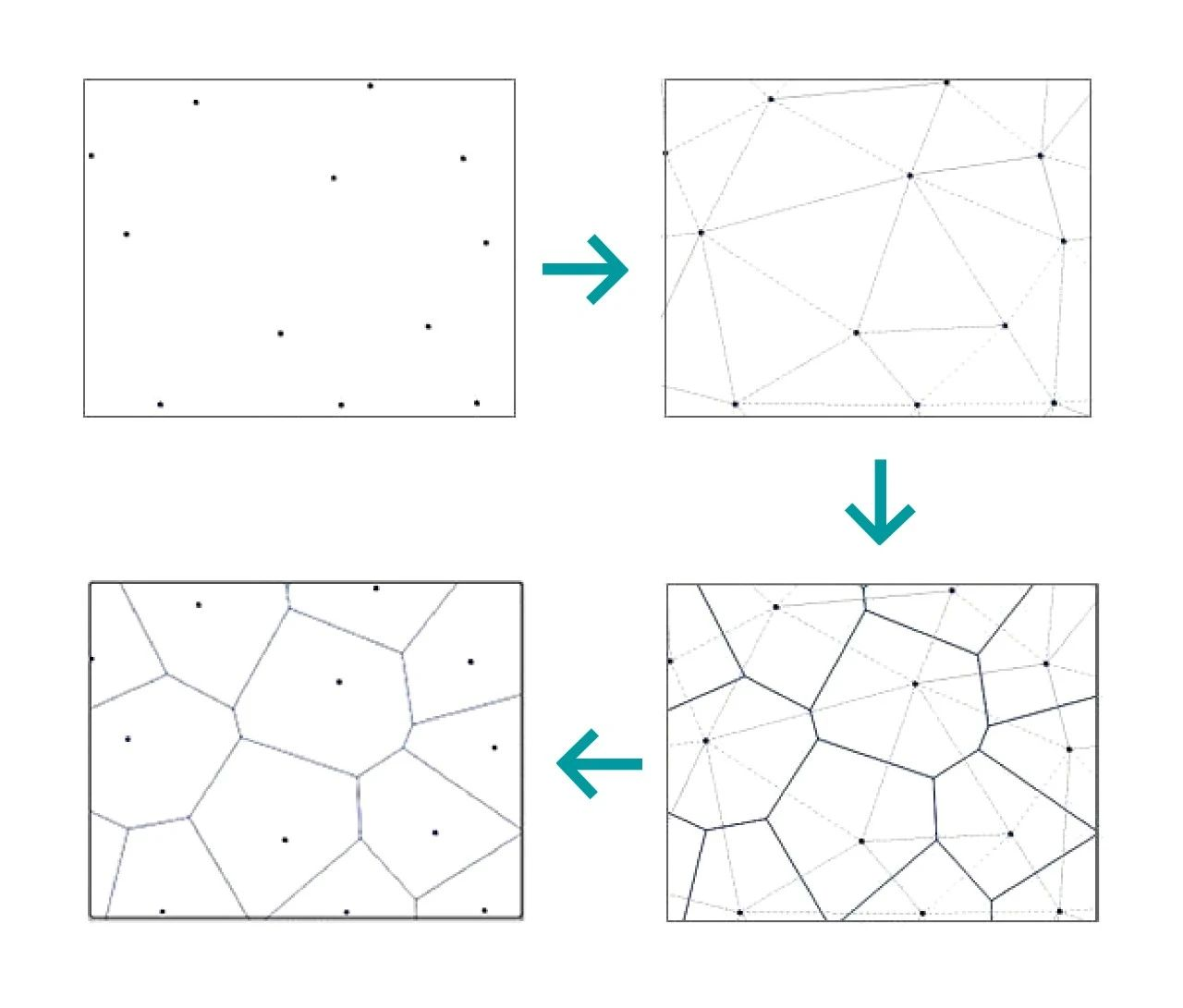
Unikátní a úžasný vzhled Tysonových polygonů má uplatnění v architektuře atd. Vzhled vodní kostky a krajinářský design parků jsou aplikovány na Tysonovy polygony.


Princip míchání světla pomocí Tysonova polygonu:
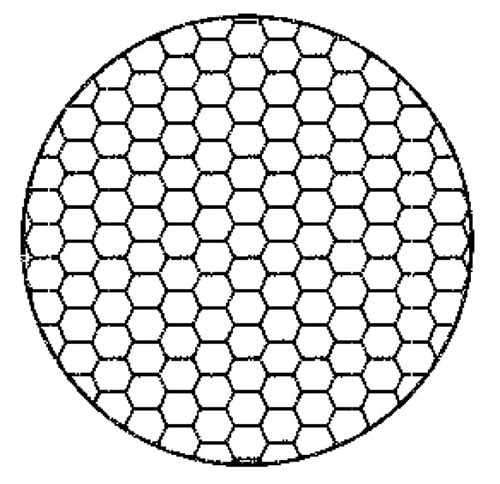
V současné době čočky na trhu často používají pro míchání světla čtyřúhelníkové, šestiúhelníkové a jiné korálkové povrchy a všechny tyto struktury mají pravidelné tvary.
Světlo vyzařované světelným zdrojem je rozděleno každou malou plochou kuličky skrz čočku a nakonec je superponováno na přijímací plochu a vytváří světelnou skvrnu. Povrchy kuliček různých tvarů mohou mapovat různé světelné skvrny, proto se používají povrchy kuliček s pravidelnými tvary, jako jsou čtyřúhelníky a šestiúhelníky. Vytvořená světelná skvrna je také tvořena superpozicí více čtyřúhelníkových a šestiúhelníkových světelných skvrn.
Thiessenův polygonální povrch korálků využívá nekonzistentní tvar každého Thiessenova polygonu k překrytí a vytvoření světelné skvrny. Pokud má povrch korálků dostatečný počet, lze je překrýt a vytvořit jednotnou kruhovou světelnou skvrnu.
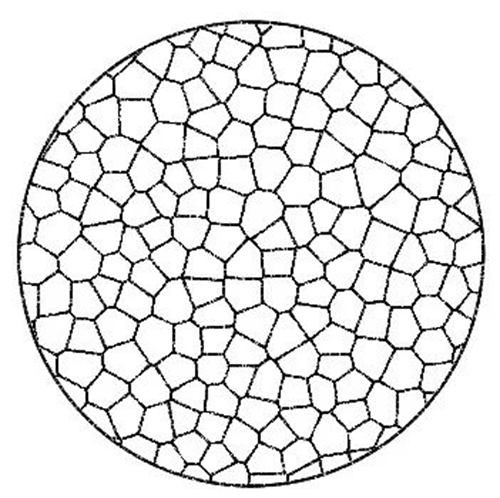
Bodový kontrast
Obrázek níže ukazuje světelnou skvrnu vytvořenou superpozicí tří povrchů perliček: čtyřúhelníku, šestiúhelníku a Thiessenova mnohoúhelníku, přičemž počet povrchů perliček a poloměr R tří typů povrchů perliček jsou stejné pod stejnou plochou vyzařující světlo.

čtyřúhelníková korálková plocha

Šestihranná korálková plocha

Tysonův polygonální korálek
Z porovnání tří světelných skvrn na obrázku výše je zřejmé, že světelná skvrna vytvořená superpozicí Tysonových polygonů na pravém obrázku se blíží kruhu a světelná skvrna bude rovnoměrnější. Je vidět, že schopnost míchání světla povrchu Tysonových polygonových korálků je silnější.
Polygonální čočka Shinland Tyson
Čas zveřejnění: 10. června 2022








